 |
|---|
| PAGE: 46 | SET: Exercises | PROBLEM: 3 |

The relation is  .
.
|
x |
y = x + 3 |
y |
(x, y) |
|
0 |
Y = 0 + 3 = 3 |
3 |
(0, 3) |
|
1 |
Y = 1 + 3 = 4 |
4 |
(1, 4) |
|
2 |
Y = 2 + 3 = 5 |
5 |
(2, 5) |
|
3 |
Y = 3 + 3 = 6 |
6 |
(3, 6) |
|
4 |
Y = 4 + 3 = 7 |
7 |
(4, 7) |
|
5 |
Y = 5 + 3 = 8 |
8 |
(5, 8) |
Express the relation as ordered pairs. 
Create a coordinate system and plot the ordered pairs.
Draw a line through the points.
Since x can be any real number, there are an infinite number of ordered pairs
that can be graphed. All of them lie on the line shown
Every real number is the x-coordinate of some point on the line.
So, the domain (x-coordinates on the line) is set of all real numbers.
Every real number is the y-coordinate of some point on the line.
So, the range (y-coordinates on the line) is also set of all real numbers.
The relation is Continuous.
Draw the vertical lines through the points. Observe that there is no vertical
line contains more than one of the points.
This graph passes the vertical line test.
For each x-value, there is exactly one y-value, so the equation  represents a function.
represents a function.
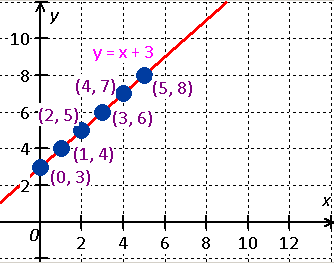
The domain (x-coordinates on the line) is set of all real numbers.
The range (y-coordinates on the line) is also set of all real numbers.
The relation is Continuous.
The equation  represents a function.
represents a function.

|
"I want to tell you that our students did well on the math exam and showed a marked improvement that, in my estimation, reflected the professional development the faculty received from you. THANK YOU!!!" June Barnett |
|
"Your site is amazing! It helped me get through Algebra." Charles |
|
"My daughter uses it to supplement her Algebra 1 school work. She finds it very helpful." Dan Pease |











