 |
|---|
SELECT PAGE NO.
No Books/Pages Are Available |
SELECT PROBLEM NO. FOR THE PAGE |
| PAGE: 83 | SET: Exercises | PROBLEM: 11 |

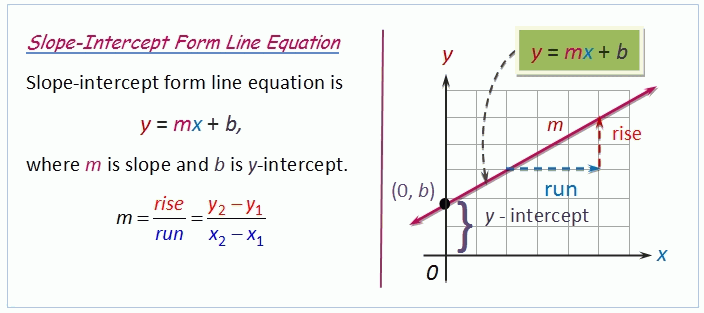
First find the slope of the line  .
.
The line in slope-intercept form y = mx + b, where m is slope and b is y-intercept.
Compare the equation with slope-intercept form and find the slope of the line.
= 
If two lines are perpendicular, the slope (m1) of one line is opposite reciprocal of the second line slope (m2). It can be represented as,  .
.
Slope of the line perpendicular to given line is 
So, slope of the new line =  .
.
The line equation in slope-intercept form is  , where m is the slope and b is the y-intercept.
, where m is the slope and b is the y-intercept.
First find the y-intercept value.
 (Substitute
(Substitute  for m)
for m)
 (Substitute 2, 0 for x, y)
(Substitute 2, 0 for x, y)
 (Multiply:
(Multiply:  )
)
Apply addition property of equality: If a = b than a + c = b + c.
 (Add
(Add  to each side)
to each side)
 (Apply additive identity property:
(Apply additive identity property:  )
)
 (Apply additive inverse property:
(Apply additive inverse property:  )
)
Substitute  for m and
for m and  for b in the Slope-intercept form line equation.
for b in the Slope-intercept form line equation.

The line equation in slope-intercept form is  .
.

|
"I want to tell you that our students did well on the math exam and showed a marked improvement that, in my estimation, reflected the professional development the faculty received from you. THANK YOU!!!" June Barnett |
|
"Your site is amazing! It helped me get through Algebra." Charles |
|
"My daughter uses it to supplement her Algebra 1 school work. She finds it very helpful." Dan Pease |











