 |
|---|
| PAGE: 574 | SET: Exercises | PROBLEM: 30 |
The function is 
.
This function represents a transformation of the graph of 
.
The transformation of function general form is 
.
Thus, here
, the graph is stretches vertically and reflected across the 
-axis.
, the graph is shifted 
units left.
, the graph is translated 
units down.
Graph:
Graph the function 
.
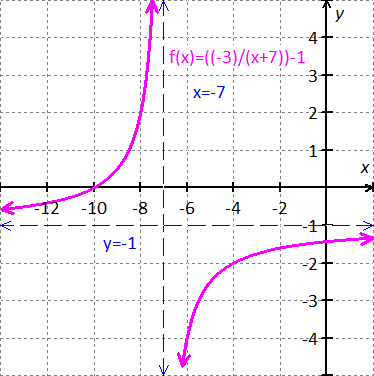
Observe the graph:
Domain is 
.
Range is 
.
Identify the asymptotes.
Identify the -values for 
is undefined.
is not defined for value of 
.
Thus, there is an asymptote at 
.
From , as a -values decrease, -values approach 
, and as -values increase, -values approach 
.
Thus there is an asymptote at 
.
Graph of the function is
The domain is 
and the range is .
The asymptote at 
.
|
"I want to tell you that our students did well on the math exam and showed a marked improvement that, in my estimation, reflected the professional development the faculty received from you. THANK YOU!!!" June Barnett |
|
"Your site is amazing! It helped me get through Algebra." Charles |
|
"My daughter uses it to supplement her Algebra 1 school work. She finds it very helpful." Dan Pease |
Simply chose a support option
  
|