 |
|---|
| PAGE: 49 | SET: Exercises | PROBLEM: 1 |

A tank holds  gallons of water.
gallons of water.
(a)
The point is  .
.
Find the slopes of the secant lines  .
.
Consider the point  .
.
At  and the corresponding the value of
and the corresponding the value of  is
is  .
.
So the point is  .
.
Slope of the two points is  .
.
The slope of the secant line  is
is  .
.
At  and the corresponding the value of
and the corresponding the value of  is
is  .
.
So the point is  .
.
The slope of the secant line  is
is  .
.
At  and the corresponding the value of
and the corresponding the value of  is
is  .
.
So the point is  .
.
The slope of the secant line  is
is  .
.
At  and the corresponding the value of
and the corresponding the value of  is
is  .
.
So the point is  .
.
The slope of the secant line  is
is  .
.
At  and the corresponding the value of
and the corresponding the value of  is
is  .
.
So the point is  .
.
The slope of the secant line  is
is  .
.
The slopes of the secant lines  are
are  and
and  .
.
(b)
Find the average of the slopes of the secant lines near to  .
.
Consider the points are near to  .
.
Points are  and
and  .
.
The slopes of the secant lines  are formed from the points
are formed from the points  and
and  is
is  and
and  .
.
The average of the slopes is 
Therefore the slope of the tangent line at  is
is  .
.
(c)
Graph :
Use the values from the table and graph the function.
(1) Draw the coordinate plane.
(2) Plot the points from the table.
(3) Connect the plotted points to a smooth curve.
(4) Draw a approximate tangent line at  .
.
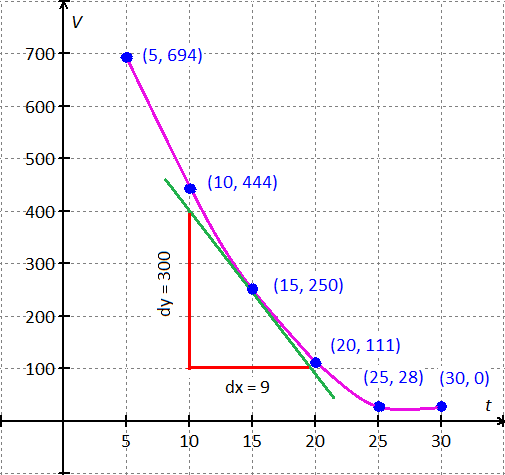
From the graph, the green line represents the approximate tangent line at  .
.
So the slope of the tangent line is  .
.
(a) The slopes of the secant lines  are
are  and
and  .
.
(b) The slope of the tangent line at  is
is  .
.
(c) The slope of the tangent line after  minutes is
minutes is  .
.

|
"I want to tell you that our students did well on the math exam and showed a marked improvement that, in my estimation, reflected the professional development the faculty received from you. THANK YOU!!!" June Barnett |
|
"Your site is amazing! It helped me get through Algebra." Charles |
|
"My daughter uses it to supplement her Algebra 1 school work. She finds it very helpful." Dan Pease |











