 |
|---|
| PAGE: 784 | SET: Exercises | PROBLEM: 29 |
Let 
be the number of the metal fastener.
Let 
be the number of the plastic fastener.
Cost of each metal fastener is 
.
Cost of each metal fastener is 
.
Total cost of six samples is 
.
Hence the constraint is 
.
Entrepreneur wants to produce at least two of each samples.
Hence the constraints are 
.
It takes 
hours to produce metal fastener and 
hours to produce plastic fastener
It does not exceed 
hours.
Hence the constraint is 
.
The objective function is .
The constraints are
Graph :
Graph the inequalities and shade the required region.
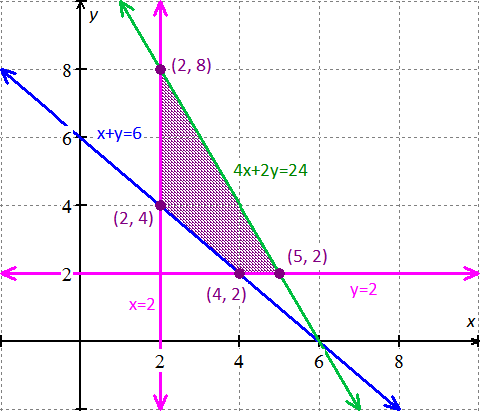
Note : The shaded region is the set of solution points for the objective function.
Observe the graph:
Tabulate the solutions of each of two system of inequalities and obtain the intersection points.
|
System of boundary equations |
|
|
|
|
| Solution (vertex points) |  |
 |
 |
|
Find the value of objective function at the solution points.
At point 
, 
.
At point 
, 
.
At point 
, 
.
At point 
, 
.
Observe the values of 
:
The minimum value of 
is
at .
Therefore, entrepreneur should make 
metal fastener and 
plastic fastener for total cost of
.
Entrepreneur should make metal fastener and plastic fastener for total cost of 
.
|
"I want to tell you that our students did well on the math exam and showed a marked improvement that, in my estimation, reflected the professional development the faculty received from you. THANK YOU!!!" June Barnett |
|
"Your site is amazing! It helped me get through Algebra." Charles |
|
"My daughter uses it to supplement her Algebra 1 school work. She finds it very helpful." Dan Pease |
Simply chose a support option
  
|