 |
|---|
SELECT PAGE NO.
No Books/Pages Are Available |
SELECT PROBLEM NO. FOR THE PAGE |
| PAGE: 106 | SET: Exercises | PROBLEM: 76 |
Find the polynomial function.
Degree of the function is 
.
Real zeros : 
.
.
Since the degree of the polynomial function is 
, it is an odd function.
The leading coefficient(
) of the polynomial function must be positive.
Because for 
odd and positive the end behavior of the polynomial function is
and
.
Let the three real zeroes are 
, and 
.
Then the factors are 
, and 
.
From the given data conclude that, there are two zeros that are not real.
Let 
be a factor, because 
has no real zeros.
Thus, the polynomial function is 
.
Graph the function 
:
Graph :
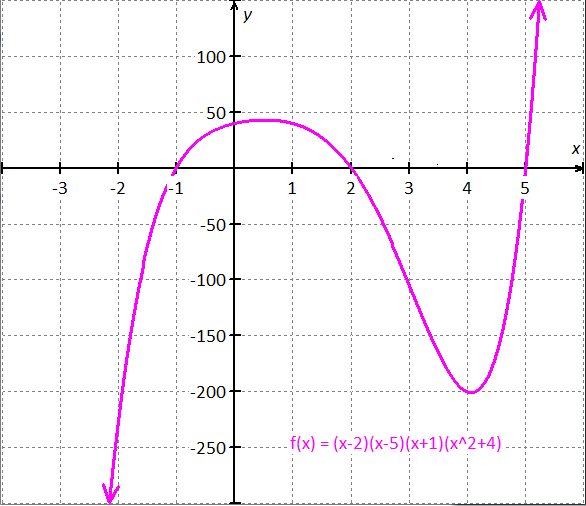
The polynomial function is .
Graph of the function is :
.
|
"I want to tell you that our students did well on the math exam and showed a marked improvement that, in my estimation, reflected the professional development the faculty received from you. THANK YOU!!!" June Barnett |
|
"Your site is amazing! It helped me get through Algebra." Charles |
|
"My daughter uses it to supplement her Algebra 1 school work. She finds it very helpful." Dan Pease |
Simply chose a support option
  
|