 |
|---|
SELECT PAGE NO.
No Books/Pages Are Available |
SELECT PROBLEM NO. FOR THE PAGE |
| PAGE: 490 | SET: Exercises | PROBLEM: 51 |
miles per hour at a bearing of 
.
miles per hour at a bearing of 
.
Draw a diagram to represent 
and 
using a scale of 
.
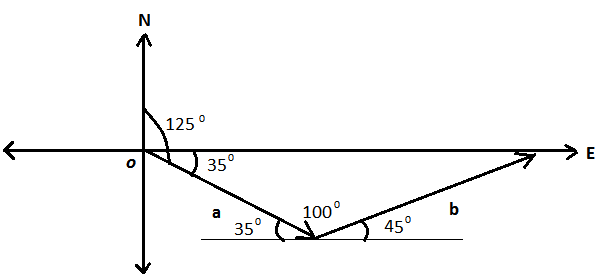
Observe the diagram :
The angle created by 
and 
- axis is 
.
Draw a horizontal where the tip of and the tail of meet, as shown in above figure.
makes a 
angle and makes a 
angle with the horizontal.
Thus, the angle created by and is 
.
Draw the resultant 
.
The three vectors form a triangle.
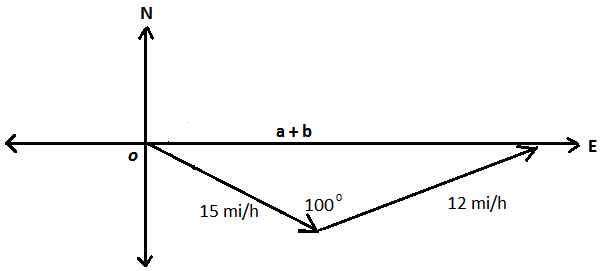
Use the law of cosines to find the magnitude of 
.
Law of cosines : 
.
Use the law of sines to find the angle opposite of .
Therefore, the angle opposite of is about 
.
To find the bearing of , subtract from .
Thus, the direction of is a bearing of 
.
Since the equilibrant vector is the opposite of resultant vector, it will have a magnitude of about 
at a bearing of about 
.
The magnitude of the quilibrant vector is about 
at a bearing of about 
.
|
"I want to tell you that our students did well on the math exam and showed a marked improvement that, in my estimation, reflected the professional development the faculty received from you. THANK YOU!!!" June Barnett |
|
"Your site is amazing! It helped me get through Algebra." Charles |
|
"My daughter uses it to supplement her Algebra 1 school work. She finds it very helpful." Dan Pease |
Simply chose a support option
  
|